Goal:
Predict the trend of Funds Inflow using historical time series data.
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import statsmodels.api as sm
from statsmodels.tsa.arima_model import ARIMA
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.stattools import adfuller as ADF
user_balance = pd.read_csv('./user_balance_table.csv')
1. EDA
#chunk1: EDA
user_balance = pd.read_csv('./user_balance_table.csv')
df_tmp = user_balance.groupby(['report_date'])['total_purchase_amt','total_redeem_amt'].sum()
df_tmp.reset_index(inplace = True)
df_tmp['report_date'] = pd.to_datetime(df_tmp['report_date'],format = '%Y%m%d')
df_tmp.index = df_tmp['report_date']
plt.figure(figsize = (12,4))
plt.plot(df_tmp['total_purchase_amt'])
plt.title('Total Purchase Amount')
plt.xlabel('Report date')
plt.ylabel('Unit(Yuan)')
plt.show()
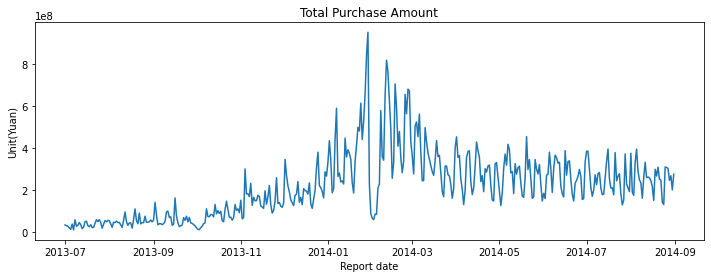
2. training, testing data preparation
#chunk2: split train and test dataset
def split_dataset():
desparse = lambda date:pd.to_datetime(date,format = '%Y%m%d')
user_balance = pd.read_csv('./user_balance_table.csv',parse_dates = ['report_date'],index_col = 'report_date',date_parser = desparse)
df = user_balance.groupby(['report_date'])['total_purchase_amt'].sum()
timeseries = pd.Series(df,name = 'value')
train_seq = timeseries['2014-04-01':'2014-07-31']
test_seq = timeseries['2014-08-01':'2014-08-10']
train_seq.to_csv('./purchase_seq_train.csv',header = True)
test_seq.to_csv('./purchase_seq_train.csv',header = True)
return train_seq,test_seq
train_seq,test_seq = split_dataset()
3. ADF Test
Aim: check whether trainning timeseries is stationary
#chunk2:
#if not stationary: try lag1 series,lag2 series
#if stationary: observe the PACF,ACF plot and select best p,q parameters for ARIMA model
def adf_check(timeseries):
seq_diff1 = timeseries.diff(1)
seq_diff2 = timeseries.diff(2)
seq_diff1 = seq_diff1.fillna(0)
seq_diff2 = seq_diff2.fillna(0)
adf0 = ADF(timeseries)
adf1 = ADF(seq_diff1)
adf2 = ADF(seq_diff2)
print('timeseries ADF test critical value is ',adf0[0],',p-value is ',adf0[1])
print('timeseries diff1 ADF test critical value is ',adf1[0],',p-value is ',adf1[1])
print('timeseries diff2 ADF test critical value is ',adf2[0],',p-value is ',adf2[1])
plt.figure(figsize = (12,9))
plt.plot(timeseries,color = 'blue',label = 'original')
plt.plot(seq_diff1,color = 'purple',label = 'diff1')
plt.plot(seq_diff2,color = 'red',label = 'diff2')
plt.legend(loc = 'best')
plt.show()
adf_check(train_seq)
timeseries ADF test critical value is -2.0639747511769917 ,p-value is 0.2592449964335145
timeseries diff1 ADF test critical value is -6.542516143607555 ,p-value is 9.270661450977037e-09
timeseries diff2 ADF test critical value is -6.720937259404168 ,p-value is 3.4845842233567905e-09
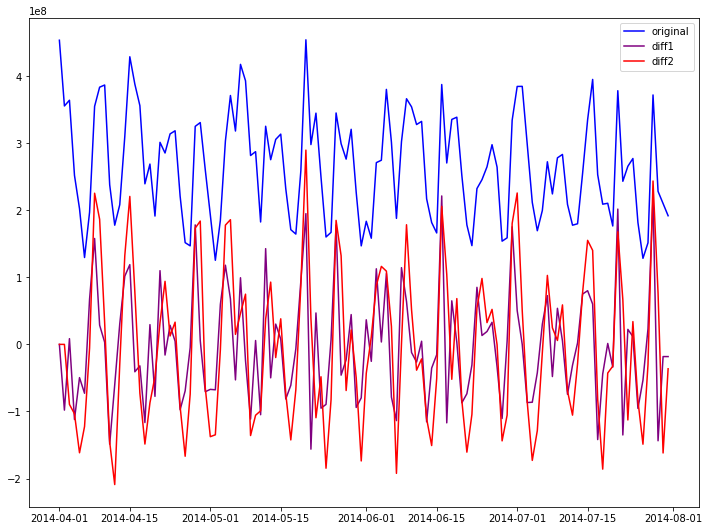
3. Hyperparatemer tuning
#chunk3: Select p,q parameters by observing PACF,ACF plot
def autocorrelation(timeseries,lags):
fig = plt.figure(figsize = (12,8))
ax1 = fig.add_subplot(211)
sm.graphics.tsa.plot_acf(timeseries,lags = lags,ax = ax1)
ax2 = fig.add_subplot(212)
sm.graphics.tsa.plot_pacf(timeseries,lags = lags,ax = ax2)
seq_diff1 = train_seq.diff(1)
seq_diff1 = seq_diff1.fillna(0)
autocorrelation(seq_diff1,20)
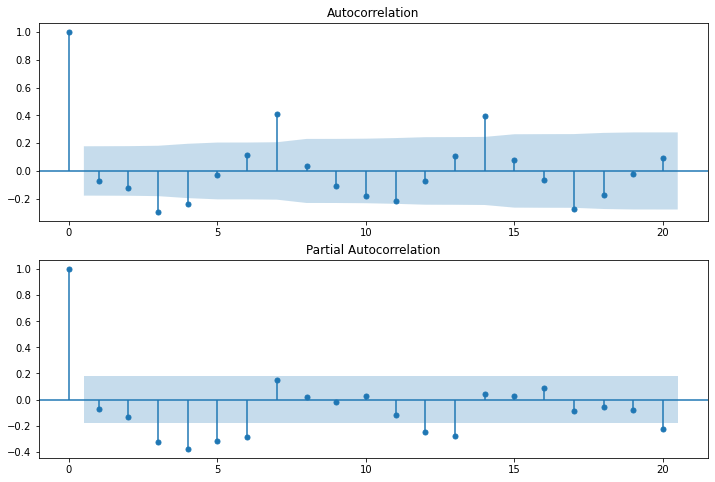
4. Seasonal and Trend decomposition using Loess(STL)
#chunk4: Seasonal and Trend decomposition using Loess(STL)
def decompose(timeseries):
decomposition = seasonal_decompose(timeseries)
trend = decomposition.trend
residual = decomposition.resid
seasonal = decomposition.seasonal
plt.figure(figsize = (12,12))
plt.subplot(411)
plt.plot(timeseries,label = 'orginal')
plt.legend(loc = 'best')
plt.subplot(412)
plt.plot(trend,label = 'trend')
plt.legend(loc = 'best')
plt.subplot(413)
plt.plot(residual,label = 'residual')
plt.legend(loc = 'best')
plt.subplot(414)
plt.plot(seasonal,label = 'seasonal')
plt.legend(loc = 'best')
decompose(train_seq)
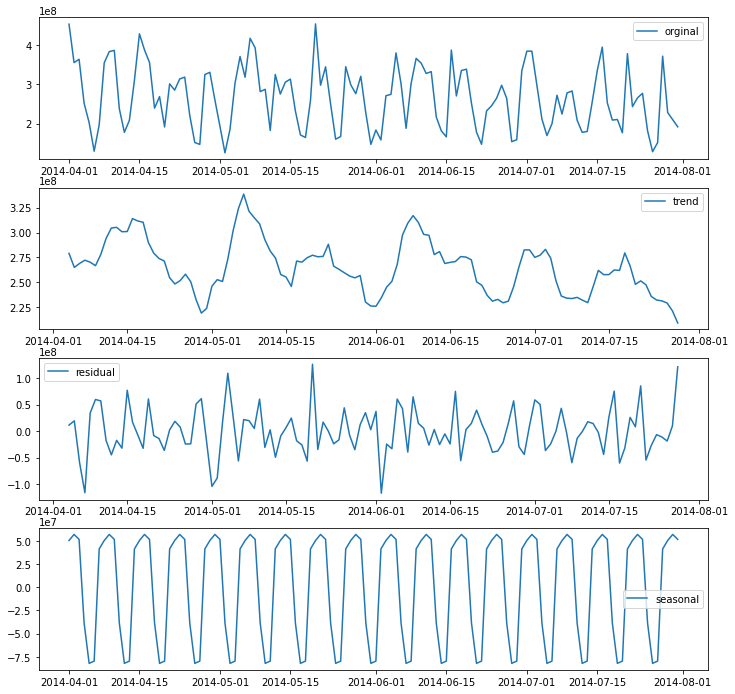
5. Recheck stationary after decomposition
decomposition = seasonal_decompose(train_seq)
trend = decomposition.trend
residual = decomposition.resid
seasonal = decomposition.seasonal
trend = trend.fillna(0)
residual=residual.fillna(0)
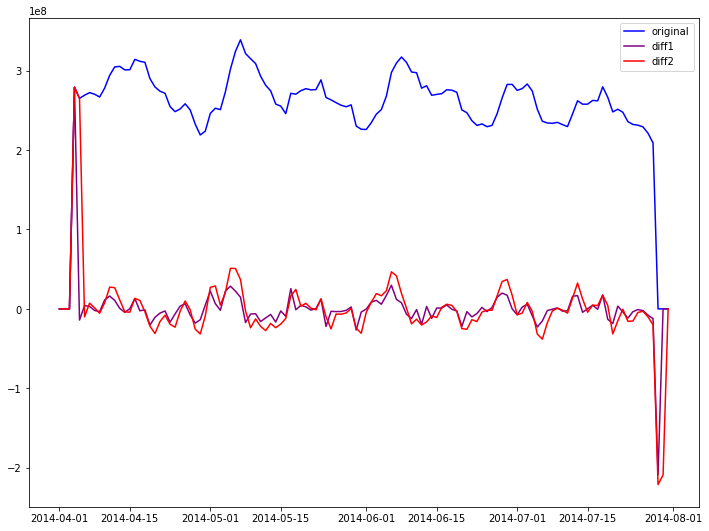
adf_check(trend)
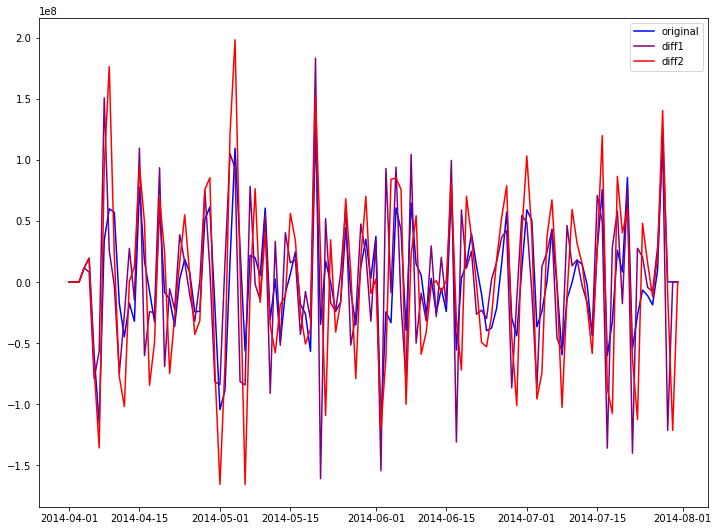
adf_check(residual)
timeseries ADF test critical value is -3.2368487584485863 ,p-value is 0.017948383665881567
timeseries diff1 ADF test critical value is -10.571816201699768 ,p-value is 7.2723798146224e-19
timeseries diff2 ADF test critical value is -4.27332487528888 ,p-value is 0.0004939083331880952
timeseries ADF test critical value is -6.290212104648341 ,p-value is 3.614727756796546e-08
timeseries diff1 ADF test critical value is -5.903150268380998 ,p-value is 2.7477376300415804e-07
timeseries diff2 ADF test critical value is -5.802841045335451 ,p-value is 4.588223613597985e-07
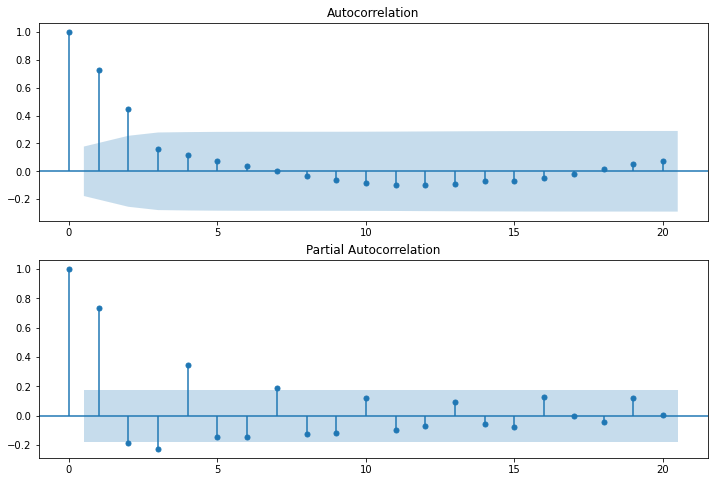
autocorrelation(trend, 20)
autocorrelation(residual, 20)
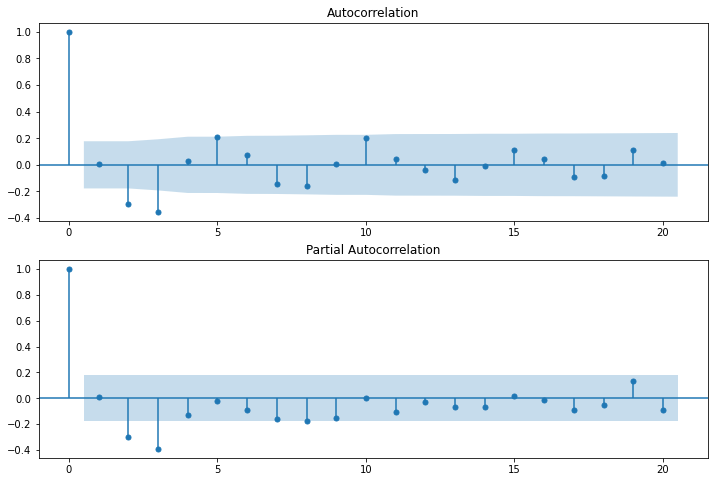
6. Model delection
#chunk5: AIC, BIC for model selection
trend_evaluate = sm.tsa.arma_order_select_ic(trend,ic = ['aic','bic'],trend = 'nc',max_ar = 4, max_ma = 4)
print('trend AIC',trend_evaluate.aic_min_order)
print('trend BIC',trend_evaluate.bic_min_order)
resid_evaluate = sm.tsa.arma_order_select_ic(residual,ic = ['aic','bic'],trend = 'nc',max_ar = 4, max_ma = 4)
print('residual AIC',resid_evaluate.aic_min_order)
print('residual AIC',resid_evaluate.bic_min_order)
trend AIC (1, 0)
trend BIC (1, 0)
residual AIC (2, 1)
residual AIC (2, 1)
#chunk3: ARIMA model building
trend_model = ARIMA(trend,(1,0,0))
trend_model = trend_model.fit(disp = False)
trend_fit_seq = trend_model.fittedvalues
trend_pred_seq = trend_model.predict(start = '2014-08-01',end = '2014-08-10',dynamic = True)
resid_model = ARIMA(residual,(2,0,1))
resid_model =resid_model.fit(disp = False)
resid_fit_seq = resid_model.fittedvalues
resid_pred_seq = resid_model.predict(start = '2014-08-01',end = '2014-08-10',dynamic = True)
7 . Model Fitting
#chunk4: Fitting Moldel
fit_seq = seasonal
fit_seq = fit_seq.add(resid_fit_seq,fill_value = 0)
fit_seq = fit_seq.add(trend_fit_seq,fill_value = 0)
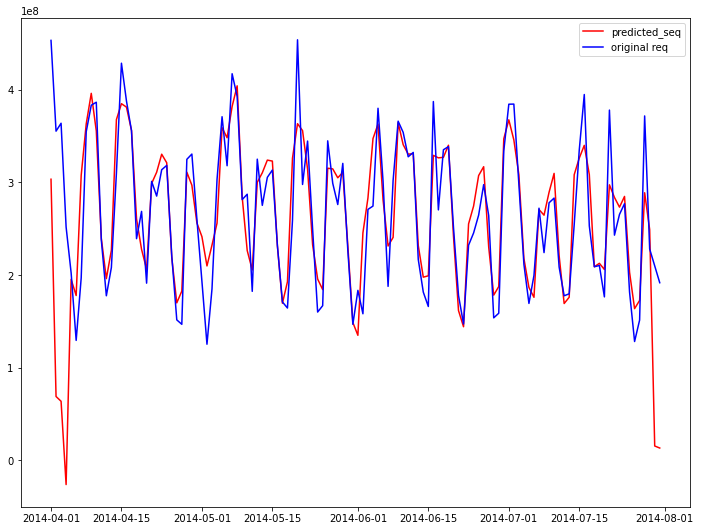
plt.figure(figsize = (12,9))
plt.subplot(111)
plt.plot(fit_seq,label = 'predicted_seq',color = 'red')
plt.plot(train_seq,label = 'original req',color = 'blue')
plt.legend(loc = 'best')
plt.show()
#making prediction
seasonal_pred = seasonal['2014-04-04':'2014-04-13']
predict_dates = pd.Series(
['2014-08-01', '2014-08-02', '2014-08-03', '2014-08-04', '2014-08-05', '2014-08-06', '2014-08-07', '2014-08-08',
'2014-08-09', '2014-08-10']).apply(lambda dates: pd.datetime.strptime(dates, '%Y-%m-%d'))
seasonal_pred.index = predict_dates
pred_seq = seasonal_pred
pred_seq = pred_seq.add(resid_pred_seq,fill_value = 0)
pred_seq = pred_seq.add(trend_pred_seq,fill_value = 0)
<ipython-input-44-02d92dd51741>:17: FutureWarning: The pandas.datetime class is deprecated and will be removed from pandas in a future version. Import from datetime module instead.
'2014-08-09', '2014-08-10']).apply(lambda dates: pd.datetime.strptime(dates, '%Y-%m-%d'))
#8. Measure Performance
#chunk5: Measure Performance
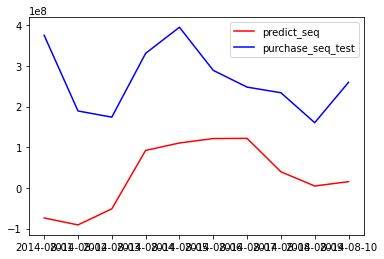
plt.plot(pred_seq, color='red', label='predict_seq')
plt.plot(test_seq, color='blue', label='purchase_seq_test')
plt.legend(loc='best')
plt.show()
def mean_absolute_percentage_error(y_true, y_pred):
y_true, y_pred = np.array(y_true), np.array(y_pred)
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
mean_absolute_percentage_error(test_seq,pred_seq)
92.45641079826935
from sklearn.metrics import mean_absolute_error
def mean_absolute_scaled_error(y_true, y_pred, y_train):
e_t = y_true - y_pred
scale = mean_absolute_error(y_train[1:], y_train[:-1])
return np.mean(np.abs(e_t / scale))
mean_absolute_scaled_error(test_seq,pred_seq,train_seq)
3.5125341730575683